教室紹介
無料相談
【数学Ⅰ 数と式】 日本一わかりやすい「絶対値の外し方」と「場合分け」 | 定額個別の櫻学舎

この春高校一年生になったAさん、数学の授業も本格的に始まり、初めて「場合分け」が出てきたようです。

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] 先生、今学校の数学で「絶対値の場合分け」に入ったんですけど、よくわかりません・・・[/speech_bubble]
[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]なるほど、じゃあ絶対値のおさらいも含めて説明していくね！[/speech_bubble]

絶対値とは、「原点までの距離」

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]Aちゃんに問題、「 3  」の絶対値は？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] えーと、「 3 」から「 0 」までの距離のことだから３！[/speech_bubble]

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]その通り！じゃあ「 – 3 」の絶対値は？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] 「 – 3 」から「 0 」までの距離だから、これも「 3 」！[/speech_bubble]

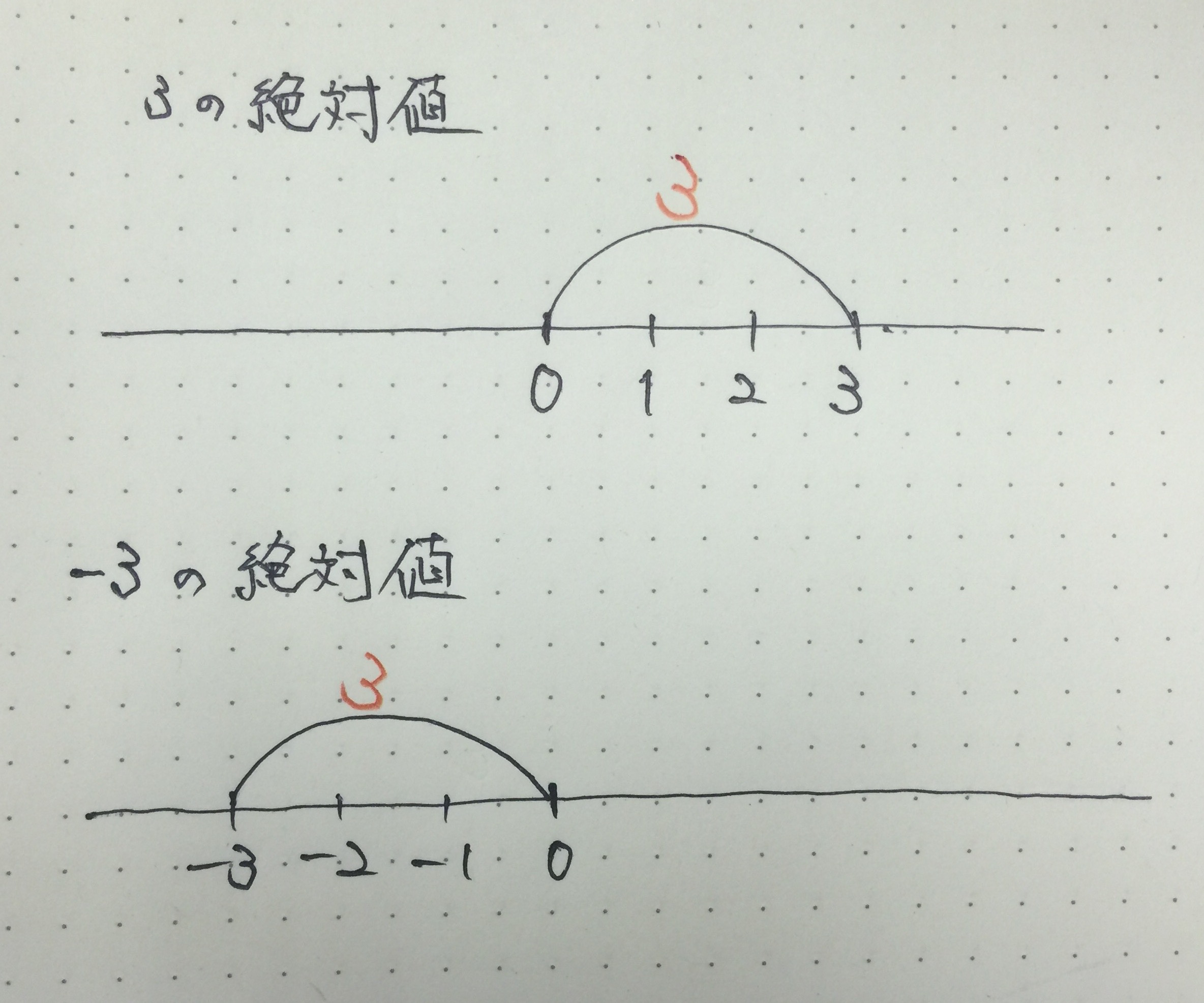
FullSizeRender-4

 

絶対値記号を使って ３ の絶対値のことを | 3 | と表します。

つまり

| 3 | = 3

| – 3 | = 3

ということですね！

絶対値記号の中が ＋ のときはそのまま外し、 − のときは − をかけて外せばいいわけです。

絶対値記号 | | の中が ➕ のときはそのまま、 ➖ のときは ➖ をかけてはずす！

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]じゃあ | √2 – 1 | はなんでしょう？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] 「 √2 」は「1.414…」だから絶対値記号の中の「 √2 – 1 」が ＋ になるので、そのまま「 √2 – 1 」ですね！[/speech_bubble]

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]素晴らしい！じゃあ | 3 – π  | はどうだろう？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] 「 π 」って円周率ですよね？ってことは「3.141592…」だから絶対値記号の中の「 3 – π 」はマイナスになるので、「 – 3 + π 」！[/speech_bubble]

あくまでも | | の中が＋のときはそのまま外し、−のときは−をかけて外します。

| √2 – 1 | = √2 – 1

| 3 – π | = – 3 + π

絶対値記号 | | の中が ＋ か − か わからない時は場合分けをする！

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]Aちゃん、いよいよ本題！ | x | はなんでしょう？ [/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] え・・・「 x 」って ＋ ？それとも − ？？[/speech_bubble]

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]じゃあ「 x 」が ＋ のときはどうなるかな？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] そのまま外れるので「 x 」です。[/speech_bubble]

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]「 x 」が−のときはどうなる？[/speech_bubble]

[speech_bubble type=”drop” subtype=”L1″ icon=”1.jpg” name=”A さん”] − をかけて外すので「 −x 」です。[/speech_bubble]

[speech_bubble type=”drop” subtype=”R1″ icon=”2.jpg” name=”私”]そういうこと！このように x の値によって答えが変化するとき、それぞれの場合によって分けて書かなきゃいけないんだよ。そしてこれを「場合分け」っていうんだ[/speech_bubble]

| x | の外し方

（ⅰ） x ≧ 0 のとき、| x | =  x

（ⅱ）x < 0 のとき、| x | = – x

このように（ⅰ）と（ⅱ）に分け、それぞれの場合における答えを書いていきます。

 

例題

| x – 2 | を求めよ。

解

（ⅰ） x – 2 ≧ 0 すなわち x ≧ 2 のとき、| x – 2 | = x – 2

（ⅱ）x – 2 < 0 すなわち x < 2 のとき、| x – 2 | = – x + 2

 

まとめ

①絶対値とは「原点までの距離」のこと。

②絶対値記号 | | の中が「 + 」の時はそのまま外し、「 – 」のときは 「- 」をかけて外す。

③絶対値記号 | | の中が「 + 」か「 – 」かわからない時は、それぞれの場合に分けて外す。

 

今日はまずこの 3 つを徹底させましょう！

高校数学で「絶対値」はいろんなところで出てきます。でもこの基本を押さえておけば、どんなに複雑になっても必ず対応できますよ^^

 

[su_box title=”本日もありがとうございました！” style=”bubbles”]本日も最後まで読んで頂いてありがとうございました！
絶対値は最初で躓く子がとても多い単元です。
インターネットで絶対値を説明しているサイトも探しましたが、どの説明も非常に分かりにくいので、今回、「絶対値の外し方」と「場合分け」というテーマで日本一わかりやすい説明を目指しました。
皆さん、理解できたでしょうか？
もし分からない所があれば、いつでもLINE、Facebook、Twitterで相談してくださいね！
原則24時間以内には返信します！勉強以外の悩みでも、何でもご相談ください！[/su_box]

[su_button url=”http://line.me/ti/p/%40mki9215t” target=”blank” style=”flat” background=”#1DCD00″ size=”11″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]LINEで質問する[/su_button]　[su_button url=”https://www.facebook.com/sakuragakusha2014/” target=”blank” style=”flat” background=”#850bd8″ size=”8″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]Facebookで質問する[/su_button]　[su_button url=”https://twitter.com/sakuragakusha” target=”blank” style=”flat” background=”#3589E2″ size=”10″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]Twitterで質問する[/su_button]

« »