【高校数学】三角関数の加法定理・倍角・半角の公式を完全攻略！覚え方＆導出まとめ

こんにちは、櫻學舎の降旗です。

高校数学で頻出の「三角関数の加法定理」「倍角の公式」「半角の公式」。

テストや大学入試でもよく問われる単元ですが、公式が多くて覚えられない…と苦手意識を持っている人も多いのではないでしょうか？

この記事では、加法定理・倍角・半角・3倍角の公式について、

「意味を理解して導出できるようにする方法」
「覚えやすい語呂やリズムで暗記する方法」

の両面からわかりやすく解説します！

θをマスター　~三角関数の加法定理、倍角と半角の公式~

高校数学でよく登場するθ。

角度を表す文字として頻出します。

苦手意識を持っている生徒さんも多いのではないでしょうか？

ここでは、加法定理、倍角と半角の公式について説明します。

三角関数の基本は既に学習済みとして解説します。

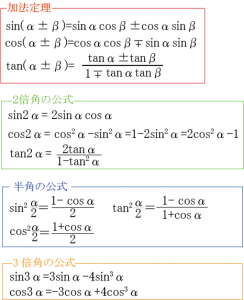
じゃん。

これは教科書にそのまま載ってるもの。

１１の公式があります。

特に数学が苦手な人に多いのが、公式が覚えられないから数学が苦手、というタイプ。

数学は三角関数に限らず、様々な公式を覚えなければなりません。

公式を確実に覚えられればテストの点数が上がるのも事実です。

しかし、いつも数学のテストで高得点を取っている人は全ての公式を確実に覚えているのでしょうか？

答えは、ノーです。

数学は、論理的に答えを導き出します。

逆に言えば、全ての答えには理由があるのです。

公三角関数の公式を覚える一番早い方法

公式一つを取ってみても、その公式は人類がたまたま見つけたものではなく、必要性から作られたものなのです。

数学でいつも高得点を取る人というのは、公式の持つ意味を理解しているので、たとえ公式を正確には覚えていなくても再び作り直すことで正確に答えを導き出せるのです。

このことから、数学ができる人は、実はあまり正確には公式を覚えてはいないのです。

数学ができる人ほど公式を覚えていない、とも言われます。

ですが、あなた方高校生が向かう目標は、大学入試。

常に時間との勝負です。

もちろん、数式の正確性は必要ですが、それと同じくらい計算のスピードも重要になってきます。

計算のスピードを上げるためには、便利な公式を正確に覚えてうまく活用することがその一つの解決策となるでしょう。

従って、高校生にとっては公式の意味を理解しつつ、公式をすぐに使えるよう、完全に暗記するのが理想と言えるでしょう。

今回取り上げた公式は１１、もちろん最終的には全て覚えて欲しいですが、加法定理の３つの式を覚えていれば、他の８つの公式は簡単に導出できます。

（加法定理の導出は結構やっかいなので、覚えてしまった方が楽です。）

以下、覚え方と導出です。

三角関数の公式の簡単な覚え方

加法定理の覚え方（sin・cos・tan）

加法定理はリズムで覚えましょう。

sinは、

sin(α＋β)＝sinαcosβ＋cosαsinβ

サインコサイン、コサインサイン。

cosは、

cos(α＋β)＝cosαcosβ－sinαsinβ

コサインコサイン、サインサイン。

符号が逆になるので注意しましょう。

sinのSはstraight、cosのCはchangeみたいな感じで。

tanは、

tan(α＋β)＝(tanα＋tanβ)/(1－tanαtanβ)

１ひくタンタン、タンたすタン。

咲いたコスモス、コスモス咲いた。コスモスコスモス、咲いた咲いた。等、語呂で覚える方法もありますが覚えやすい方を選んでください。

2倍角の公式の覚え方と導出法

残念ながら、２倍角の覚え方はありません。

自分で面白い覚え方を見つけるか、形で覚えましょう。

導出は、とてもシンプルです。

２倍角とはつまり、sin2θ= sin(θ+θ)ということです。

これはそのまま加法定理が使えそうですね。

sinの加法定理のα, ßの両方をθに代えてみてください。

10秒で導出できます。

cos, tan も同様です。

cos2αは式が長いですが、これは(sinα)², (cosα)²をそれぞれ1-(cosα)², 1-(sinα)²に変換して整理しているだけです。

ですが、これらの式を全て覚えるのは重要です。

tan2αは加法定理からでも、またはtan2α=sin2α/cos2αからでも簡単に導出できます。

半角の公式の覚え方と導出法

これも覚え方がありません。

導出にはcosの２倍角の公式を使います。

２倍角の公式をsinα、あるいはcosαについて解いているだけです。

tanの半角は、(tanα)²=(sinα)²/(cosα)²から導出します。

3倍角の公式は語呂で覚えよう！

この式は語呂で覚えるのが有効そうです。

sin3α=3sinα-4(sinα)³

ミシン引くよ、シンさん。

cos3α=4(cosα)³-3cosα

陽子さん引く神輿（みこし）。

ポイントはみこしの最後を少し訛らせてミコスと覚えるところ。

田舎育ちの陽子さんがお祭りで張り切って神輿を引いている情景が思い浮かびます。

櫻學舎の数学指導

三角関数のように公式が多く、難しく感じやすい単元でも、櫻學舎では「なぜそうなるのか」「どう使えばいいのか」を丁寧に教えます。

論理的な理解を重視

ただ暗記するのではなく、公式の成り立ちや使い方の背景をしっかり解説します。

「公式の意味がわかるから、忘れても導ける」── そんな学びを目指しています。

一人ひとりに合わせた指導

櫻學舎では、個別または少人数制の授業で、生徒の理解度に応じた解説と問題演習を行います。

• 「計算ミスが多い」生徒には、ミスの原因と解決策を丁寧に

• 「理解はできているがスピードが遅い」生徒には、演習量を強化

など、学力の“つまづきポイント”に合わせてカリキュラムを調整しています。

定期テストも、入試対策も

三角関数は高校1・2年で学ぶ内容ですが、共通テストや私大・国公立の入試問題でも頻出分野です。

櫻學舎では、日々の学校授業のフォローから、模試・入試レベルの演習まで幅広く対応しています。

塾だからこそできる、「覚え方」の工夫もたくさん！

• 加法定理のリズムや語呂合わせ

• 倍角・半角の導出テクニック

• 3倍角のユニークなイメージ法

など、暗記が苦手な生徒でも覚えやすい工夫を取り入れているのも特長です。

まとめ

以上、公式いろいろの覚え方・導出でしたが、いかがでしたでしょうか？

θはマシターできましたか？

数学は正確さとスピードが要求されます。

高校数学をマスターできるよう、公式を丸暗記する方法、公式の持つ意味を理解する方法、２つの道でチャレンジしてみては？

出典

加法定理　公式・証明・覚え方