こんにちは！櫻學舎講師の菊池涼です！
今回は中学校に入って初めて習う「方程式」について「解き方」ではなく、まずその「立て方」について学んでいきたいと思います。
ポイントは”両辺の単位”をそろえるです。
方程式の定義は「変数の特定値についてだけ両辺が等しくなる等式」とのことですが…何を言ってるのかさっぱりですね。
要は文字が含まれていても左辺と右辺が同じ数になれば良いということで、中学校では次数が１つの一次方程式を主に習います。
といってもよく分からないのでざっくり文字の含まれた方程式を立てると
X＋８＝９
この時X＝１で両辺の数が等しくなり方程式が成り立ちます。
このような式のことを方程式と呼びます。
では次の項で式の立て方を見ていきましょう。
例題
チョコレートがあり、１人に５個ずつ分けようとすると３個足りず、１人に２個ずつ分けようとすると３個余る。子供の人数は何人か？また、チョコレートは何個あるか？
この方程式を立てるとき、まず何を文字、つまりはｘと置くのか決めます。
といっても難しいことではなく、求めたいものを文字にすればよいのでまずは子供の人数をｘにしましょう。
まず、方程式の右辺と左辺が同じ事柄を示しているようにしなければなりません。
今回の場合はチョコレートの個数です。
左辺＝「１人に５個ずつ分けようとすると３個足りない」＝５ｘ－３
右辺＝「１人に２個ずつ分けようとすると３個余る」＝２ｘ＋３
で、右辺も左辺もチョコレートの個数を示しているので両辺が同じ事柄を示していることになり、方程式が立ちます。
つまり
「１人に５個ずつ分けようとすると３個足りない」＝「１人に２個ずつ分けようとすると３個余る」
５ｘ－３＝２ｘ＋３
になります。
この式を解くとｘ＝２
つまり、子どもは２人だったということが分かります。
左辺の式も右辺の式もチョコレートの個数を示しているのでどちらにｘ＝２を代入しても答えが７になりチョコレートが７個あったことが分かります。
どの問題でもこのように考えていけば式を立てることができます。
今回の場合は個数で両辺を等しくしました。
次は道のり、速さ、時間の例で見てみましょう。
みはじの問題、つまりは道のり、速さ、時間の問題を解いていきましょう。
結構な人がここでつまずくと思います。でも式の両辺で単位をそろえることを意識すればイチコロです！
まず基本中の基本ですが
速さ＝道のり ÷ 時間
時間＝道のり ÷ 速さ
道のり＝速さ × 時間
です。
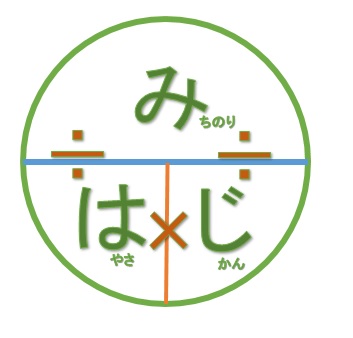
（http://ppp-kumanomuh.air-nifty.com/gakkencaimitonishimigawa/2014/03/post-88cb.html）
この図で覚えている人も多いと思います。覚えていない人もぜひ覚えてください。
例題
A町からB町は3000ｍです。タロウ君はA町からB町に向かって、分速80ｍの速さで歩き、イチロウ君はB町からA町に向かって、分速70ｍの速さで歩きます。２人が同時に出発したとき、２人は何分後に出会いますか？
まずここで、２人が何分後に出会うのか聞かれているので、時間をｘにします。
次に式の両辺の単位を決めます。
問題文から分かっていることを調べると道のり3000ｍ、タロウ君の歩く速さ分速80ｍ、イチロウ君の歩く速さ分速70ｍが分かります。
ここで、みはじの式や表からも道のり＝速さ × 時間が分かります。つまりこの式の単位は道のり（ｍ）です。
まずタロウ君の歩いた道のりは80ｘ
次にイチロウ君の歩いた道のりは70ｘ
（2人が同時に出発して出会うので歩いた時間は2人ともｘ分です。）
この道のりが3000ｍだから
80ｘ＋70ｘ＝3000
150ｘ＝3000
ｘ＝20
よって二人が出会うのは20分後だということが分かります。
これらの問題は様々なバリエーションがあるので問題数をこなして慣れていきましょう！
方程式を立てるときに一番重要なのは左辺＝右辺になることです。
つまりは両辺の単位がそろわなければいけないので、そこに注意して方程式を立てましょう。
パッと見て分からなくてもよく考えれば絶対に解けます。全問正解を目指しましょう！