[mathjax]
みなさんこんにちは、櫻學舎の小林亨です。今日は三角関比についてお話ししたいと思います。
三角比は「直角三角形の鋭角がある角度θであるときの辺の長さの比」というものです。
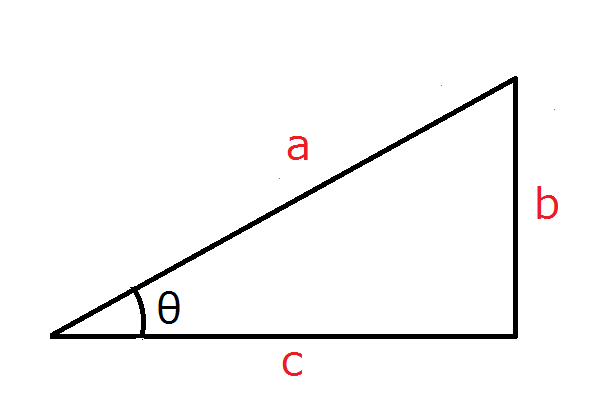
この図の直角三角形では、
$$ \sinθ=\frac{b}{a} $$ $$\cosθ=\frac{c}{a} $$ $$ \tanθ=\frac{b}{c} $$
の三つが公式となります。
sinを筆記体で書くと
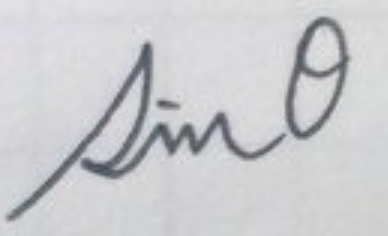
このように書きます。sinのsの字を三角形に当てはめると
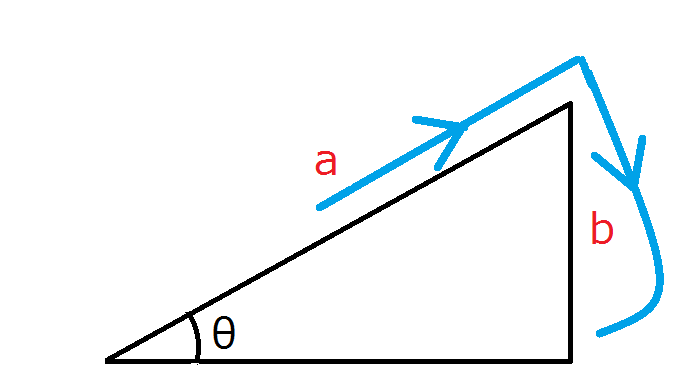
となり、 $$\sinθ=\frac{b}{a}$$ と覚えることができます。
同様に
cosのcを三角形に当てはめると
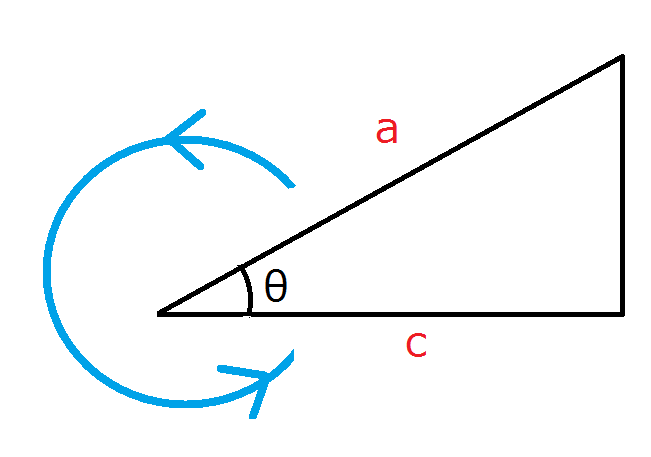
となり、 $$\cosθ=\frac{c}{a} $$
tanθを筆記体で書くと
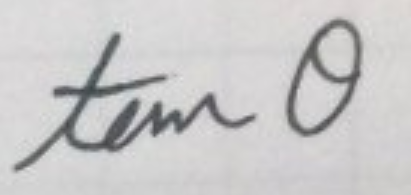
と書けます。tanのtを三角形に当てはめると、
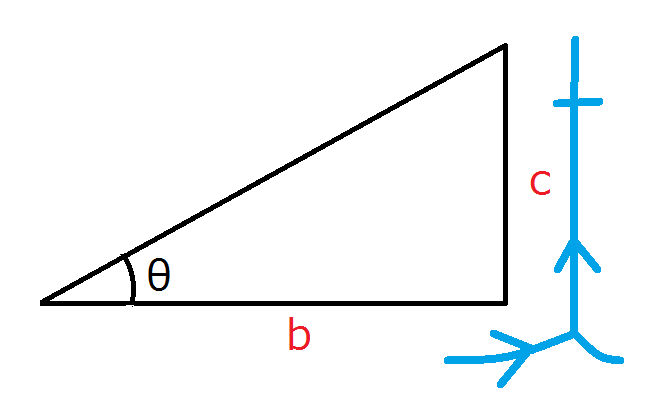
となり、$$ \tanθ=\frac{c}{b} $$
覚えておくべきθの値は、０°、３０°、４５°、６０°、９０°の５つです。これを表にすると
| θ | 0゜ | 30゜ | 45゜ | 60゜ | 90゜ |
| sinθ | 0 | $$ \frac{1}{2} $$ | $$\frac {\sqrt{2}}{2} $$ | $$\frac {\sqrt{3}}{2} $$ | 1 |
| cosθ | 1 | $$\frac {\sqrt{3}}{2} $$ | $$\frac {\sqrt{2}}{2} $$ | $$ \frac{1}{2} $$ | 0 |
| tanθ | 0 | $$ \frac{1}{\sqrt{3} } $$ | 1 | $$ \sqrt{3} $$ | – |
となります。このまま覚えてもいいのですが、少し覚えずらいので
| θ | 0゜ | 30゜ | 45゜ | 60゜ | 90゜ |
| sinθ | $$\frac {\sqrt{0}}{2} $$ | $$\frac {\sqrt{1}}{2} $$ | $$\frac {\sqrt{2}}{2} $$ | $$\frac {\sqrt{3}}{2} $$ | $$\frac {\sqrt{4}}{2} $$ |
| cosθ | $$\frac {\sqrt{4}}{2} $$ | $$\frac {\sqrt{3}}{2} $$ | $$\frac {\sqrt{2}}{2} $$ | $$\frac {\sqrt{1}}{2} $$ | $$\frac {\sqrt{0}}{2} $$ |
| tanθ | 0 | $$ \frac{1}{\sqrt{3} } $$ | 1 | $$ \sqrt{3} $$ | – |
このようにします。こうすると、sinθ,cosθの値をすべて $$\frac {\sqrt{●}}{2} $$（●は０～４）の形で表すことができます。
覚え方として
サインの「さ」→最初から（０°→９０°）●に０→４の順番で数字を当てはめる。
コサインの「こ」→後退しながら（９０°→０°）●に０→４の順番で数字を当てはめる。
tanθに関しては特別な覚え方はありませんが、sinθとcosθを覚えていれば、$$ \tanθ=\frac{\sinθ}{\cosθ} $$で導き出すことができます。
sinθ、cosθ、tanθはそれぞれの頭のローマ字と直角三角形の形が対応している。
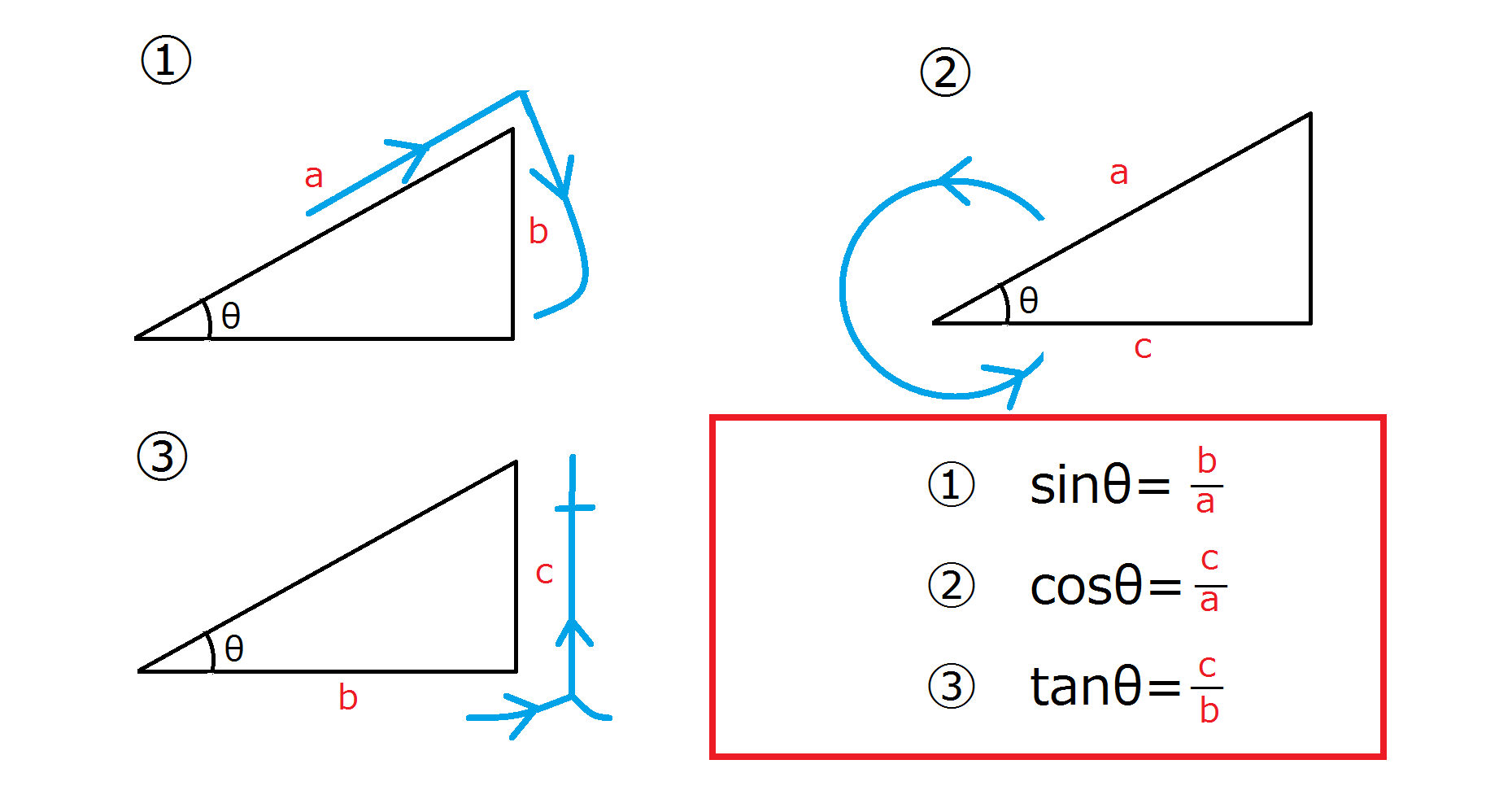
θの値が０°→３０°→４５°→６０°→９０°のとき、sinθは$$\frac {\sqrt{●}}{2} $$（●＝０→４）
cosθは$$\frac {\sqrt{●}}{2} $$（●＝４→０）となります。
これらはのことは高校でも使う基礎の部分なので、ぜひ覚えてください。