[mathjax]
こんにちは！櫻學舎講師の菊池涼です！
今回は最近生徒にも質問され、僕自身も習いたての頃は分かりにくかった「内分と外分」について解説していきたいと思います！
理解するコツは「図を書いて考える」ことです。
(今回の記事でmとnは正の数とします)
まず内分の定義を確認してみると
線分AB上の点Pが
AP : PB = m : n
を満たすとき、点Pは線分ABをm:nに内分するという。
実際に図に表してみると
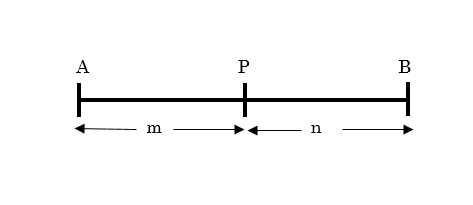
内分は線分ABの「内」部で「分」けるから内分。
これは分かりやすいと思います。
次に外分の定義を確認しましょう
線分ABの延長線上の点Qが
AQ : QB = m : n (m ≠ n)
を満たすとき、点Qは線分ABをm:nに外分するという。
これも図に表してみると
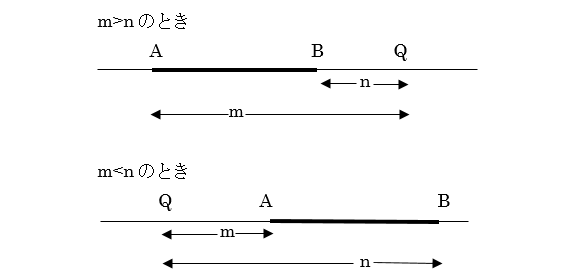
あらら…mとnの大小によって二つに分かれてしまいました。大体の人がこの外分でつまずきます。
そもそも外分は線分ABの「外」部で「分」けるから外分。外で分けなければならなくなるのは線分ABの中で分けられ無いほど大きな比になっているときです。
例えば線分ABの間が5のとき、AQとQBを8対3に分けろと言われてもAとBの間が5しかないから線分の内部だけでは分けられません。そんな時はAQの方がQBよりも大きな値を取るのでAから遠い、Bよりも右の外部に点Qを取ります。反対にQBの方がABよりも大きな値だったらAよりも左の外部に点Qを取ります。
問題文をパッと見て分からなかったら実際に数直線を書けば案外答えは簡単に出ます。図を書いて考えましょう！
座標の求め方、実はめちゃくちゃ簡単なんです。
なぜなら第1項、2項で学んだ比を使った計算をすれば求められるから。
まず内分ですが第1項で使った図をもう一度使いましょう
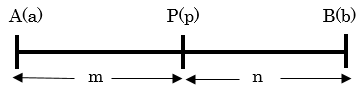
まずa<bのとき、\( AP=p-a \)、\( PB=b-p\) である。
\( AP : PB = m : n \) より
\( (p-a) : (b-p) = m : n \)
内かけ外かけで
\( n ( p – a ) = m ( b – p ) \)
したがって
\( p = \frac{ na + mb }{ m + n } \)
a<bのときも同様にして同じ座標が得られます。
外分の座標も内分と同じ要領で得られます。
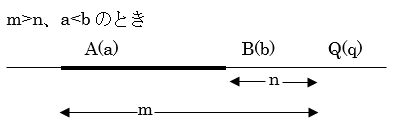
点Bは線分AQを \( (m-n ) : n \) に内分するから
\( b = \frac{ na + ( m – n )q }{ (m-n) + n } \)
したがって
\( q = \frac{ -na + mb }{ m – n } \)
m<n、a>bのときも同様にして同じ解が得られます。
中点の座標は内分を1:1にしたものだから
\( \frac{ a + b }{ 2 } \)
になります。
座標の求め方は公式を覚える必要がありません。覚えたほうが計算が早いかもしれませんが忘れてしまっても今回学んだように比で計算すれば簡単に求めることができます。ここでも図を書いて考えることを忘れずに！
問題
1 数直線上の3点A(3),B(8),C(5)について(1),(2)の空欄に適する数または用語を入れよ。
(1)点Cは線分ABを[ ]:[ ]に[ ]する。
(2)点Aは線分CBを[ ]:[ ]に[ ]する。
2 2点A(2),B(8)を結ぶ線分ABについて、次の座標を求めよ。
(1)1:2に内分する点C
(2)3:5に外分する点D
(3)中点M
回答
1
(1)点Cは線分ABを[ 2 ]:[ 3 ]に[ 内分 ]する。
(2)点Aは線分CBを[ 2 ]:[ 5 ]に[ 外分 ]する。
2
(1) 4
(2) -7
(3) 5
今回は内分と外分について取り上げましたがいかがだったでしょうか？
理解するコツは図を書いて考えることです。今回の場合は数直線を活用して答えを導き出しましょう！
以上「図と一緒に考える内分と外分」でした！
[su_box title=”内分外分は「図」を書いて考えよう！” style=”bubbles”]本日も最後まで読んでいただいてありがとうございました！内分と外分につまづいている人は少なくないはず。。。でも、そんな時には、今回紹介した「図を書いて考える」ということをやってみてくださいね！ほかにも疑問点があればいつでも質問してください！原則24時間以内には返信します！勉強以外の悩みでも、何でもご相談ください！[/su_box]
[su_button url=”http://line.me/ti/p/%40mki9215t” target=”blank” style=”flat” background=”#1DCD00″ size=”11″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]LINEで質問する[/su_button] [su_button url=”https://www.facebook.com/sakuragakusha2014/” target=”blank” style=”flat” background=”#850bd8″ size=”8″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]Facebookで質問する[/su_button] [su_button url=”https://twitter.com/sakuragakusha” target=”blank” style=”flat” background=”#3589E2″ size=”10″ center=”yes” radius=”round” icon_color=”#ffffff” text_shadow=”0px 0px 0px #000000″]Twitterで質問する[/su_button]