【電気回路の計算問題】苦手克服のために意識してほしい3つのポイント｜例題付きで徹底解説！

こんにちは、山口です。

電気回路の計算問題って、なんだか難しそう…そう感じていませんか？
中学・高校の理科や物理で登場する「オームの法則」や「直列・並列回路」は、多くの受験生がつまずくポイントの一つです。

でも実は、基本の考え方と問題の「解き方の順序」さえ押さえれば、誰でも正しく解けるようになります。

この記事では、電気回路を解くうえで意識してほしい「3つの鉄則」とともに、実際の例題を使ってスムーズな解き方の流れを解説します。

「苦手」を「得意」に変える第一歩を、ここから一緒に踏み出しましょう！

まず意識したい3つの基本

電気回路の問題は、「なんとなく難しそう…」と感じる人が多い分野ですが、基本的な考え方さえ身につければ、確実に解けるようになります。

特に大切な3つのポイントを、最初に紹介します。

① 回路図を描き、図の中に値を書き込む

電気回路の問題では、回路図もしくは装置全体の図が与えられていると思います。

回路の様子が言葉でしか与えられていない不親切な問題もあるかもしれません。

回路図が与えられている場合はその図を使っていいと思いますが、それ以外の場合は自分で回路図を描くことをおすすめします。

そして、その図に与えられた値を書き込むようにしてください。

そうすることで何がわかっていて何がわかってないのか理解できるので、問題を解く道筋を立てやすくなります。

②「電圧・電流・抵抗」のうち2つがわかっているところを探す

次に電気抵抗、電流、電圧のうち２つがわかっているものを探します。

２つがわかれば、オームの法則

$$V=RI$$

\begin{array}{@{}1} V=電圧\\ R=電気抵抗 \\I=電流\end{array}

に値を入れて残りの値が求めます。

オームの法則で求められる値が求め終わったら、

「直列回路の各抵抗に流れる電流は全体の電流と等しい」

「並列回路の各抵抗にかかる電圧は全体にかかる電圧に等しい」

などの回路の性質を考えましょう。

そうしたら、回路の性質で求めた値を使い、さらにオームの法則を使って別の値を求めていきましょう。

オームの法則→回路の性質→オームの法則→回路の性質→・・・・・・

というような流れで考えていきましょう。

③ 複雑な回路は「合成抵抗」に置き換えてシンプルにする

値自体は１，２の流れで求めることができます。

しかし、発展問題では抵抗が増えたりするなどして回路が複雑になります。

このようなときは、２つ以上の抵抗を１つの抵抗とみなして考えましょう。

シンプルな回路とみなして全体像を考え、そのあとに１つの抵抗とみなした部分を詳しく考えると問題を考えやすくなると思います。

ここで、1つ問題を解いてみましょう。

例題1

問題：抵抗aの電気抵抗を求めてみましょう。

①図を描いて、値を整理しよう

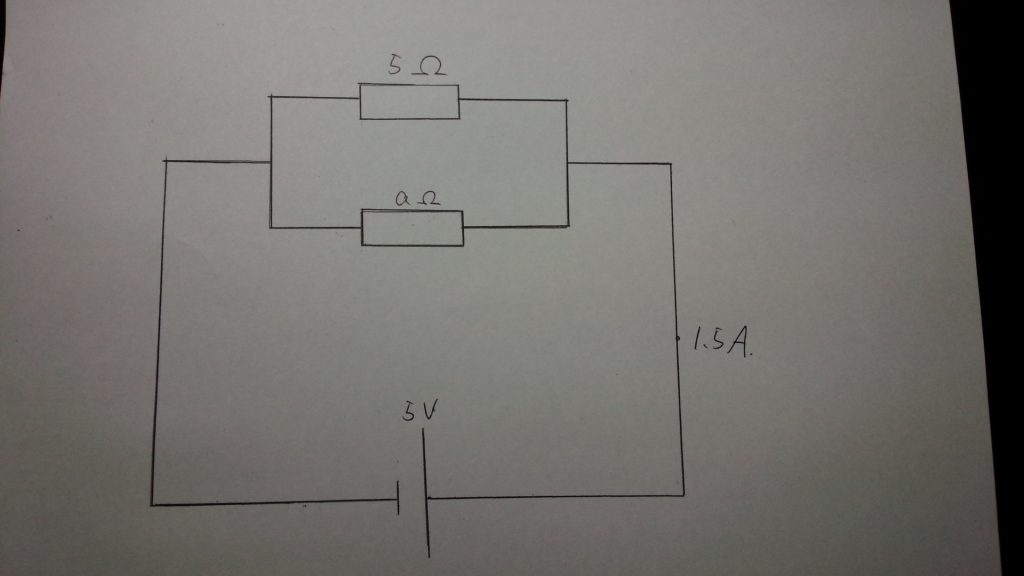
まずは回路図を描き、電源（電圧）や各抵抗の位置関係、分かっている値（電流や抵抗値）を書き込んでいきます。

②並列回路の性質を使って電圧を考える

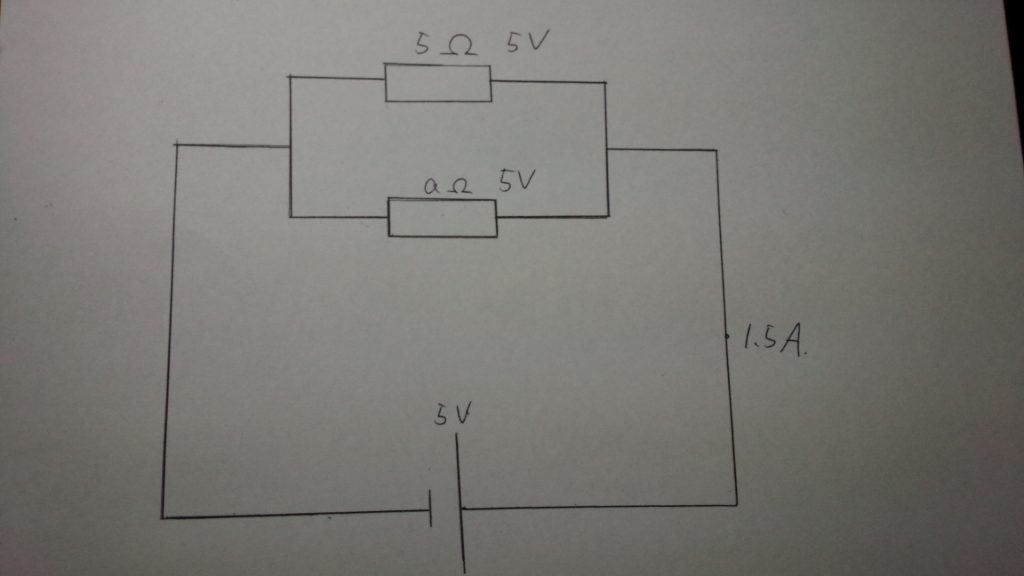
並列回路の性質から、２つの抵抗それぞれに５Ｖの電圧がかかることが分かります。このとき、抵抗のそばにわかった電圧の値を書き込むことがポイントです。

③オームの法則で電流を求める

ここで５Ωの抵抗に注目すると、電気抵抗と電流が分かっているので、オームの法則から

$$５(v) \div　５(Ω)＝　１（Ａ）$$

電流が １Ａとわかります。

また、\(a\)の抵抗の電気抵抗を\(a\)(Ω)とすると、\(a\)の抵抗に流れる電流は

$$５(v) \div　a(Ω)＝　\frac{5}{a}（Ａ）$$

となります。

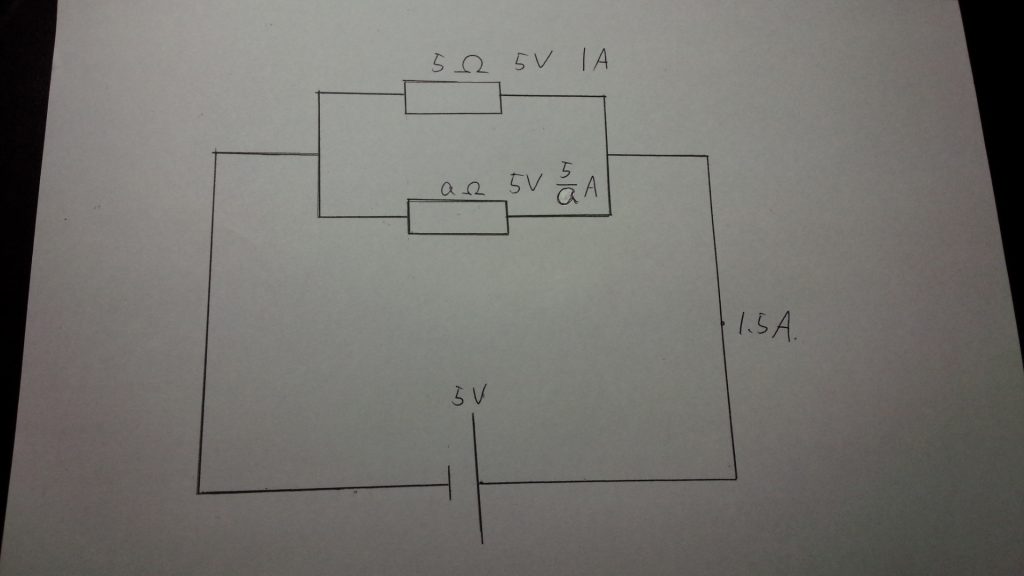
④回路全体の電流から連立方程式を作る

並列回路であるから、

$$５Ωの抵抗に流れる電流　＋　aの抵抗に流れる電流　＝　回路全体に流れる電流$$

$$1(A) +　\frac{5}{a}（Ａ）＝　1.5（Ａ）$$

よって。\(a = １０\)（Ω）　と求めることができます。

次はもっと複雑な問題にチャレンジしてみましょう。

例題2

問題：R3の電気抵抗を求めてみましょう。

①図を描いて値を書き込む

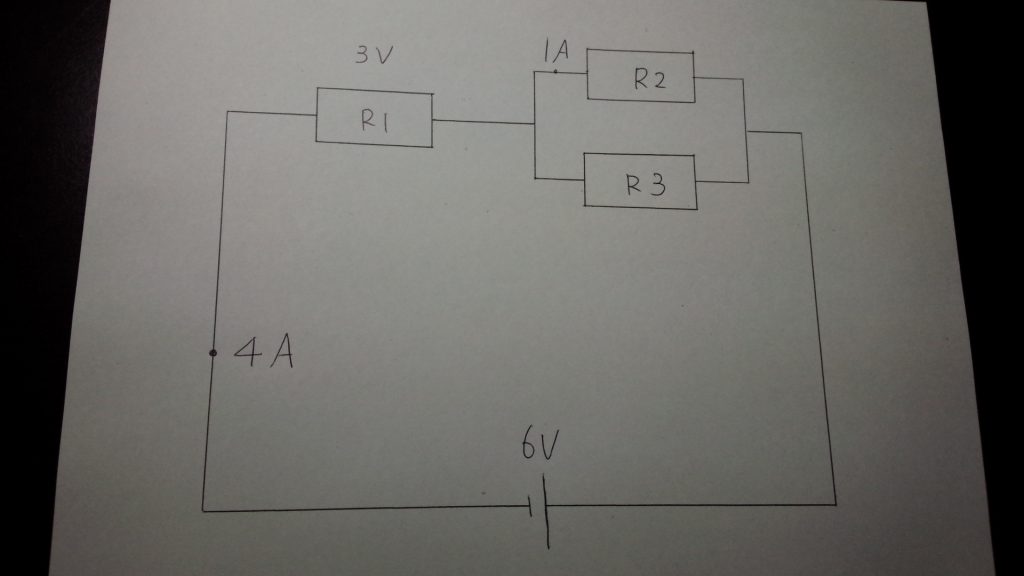
この問題でもまずは図を描きましょう。並列につながった２つの抵抗と一つの抵抗が直列につながっていますね。

②右側の並列回路を「1つの抵抗」とみなす

まず、右側の並列回路全体に流れる電流を求めます。

Ｒ１の電気抵抗も求めることができますが、Ｒ３を求めるにあたって必要ではないため求めなくても大丈夫です。

ここで重要なのが、右側の並列回路を１つの抵抗と見ることです。

ちょっと難しい考え方ですが、このことによってこの複雑な回路全体ををシンプルな直列回路として見ることができます。

③電圧・電流を順に求めていく

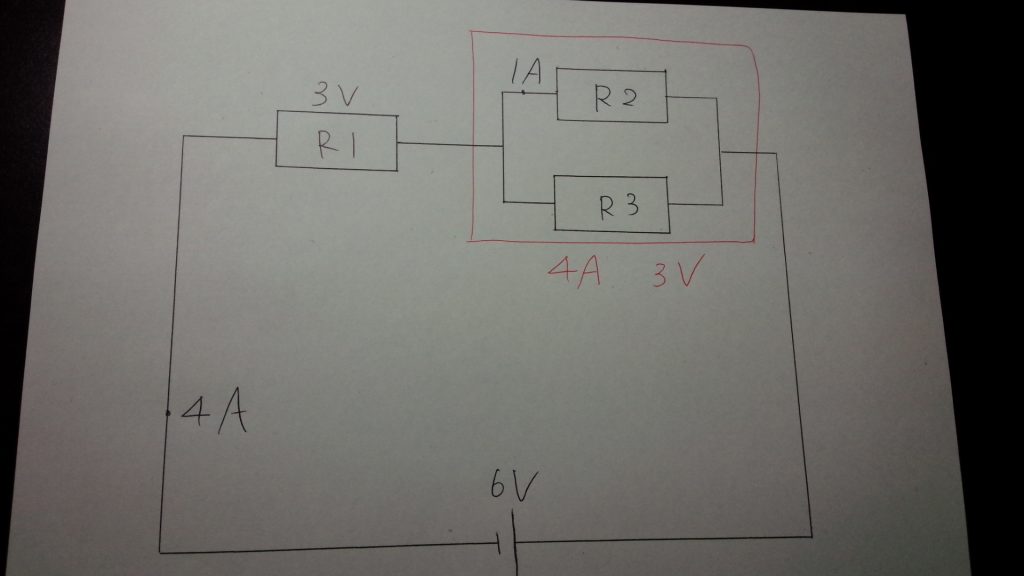
直列回路の性質から、並列回路（赤で囲った部分）にかかる電圧は４Ａとわかります。

また、並列回路の性質から

$$Ｒ２に流れる電流　＋　Ｒ３に流れる電流　＝　４（Ａ）$$

より、Ｒ３に流れる電流は１(Ａ)とわかります。

また、直列回路の性質から、並列回路にかかる電圧は

$$６（Ｖ）　－　３（Ｖ）　＝　３（Ｖ）$$

とわかります。

また、並列回路の性質からＲ３にかかる電圧も３(Ｖ)とわかります。

④オームの法則でR₃の抵抗を求める

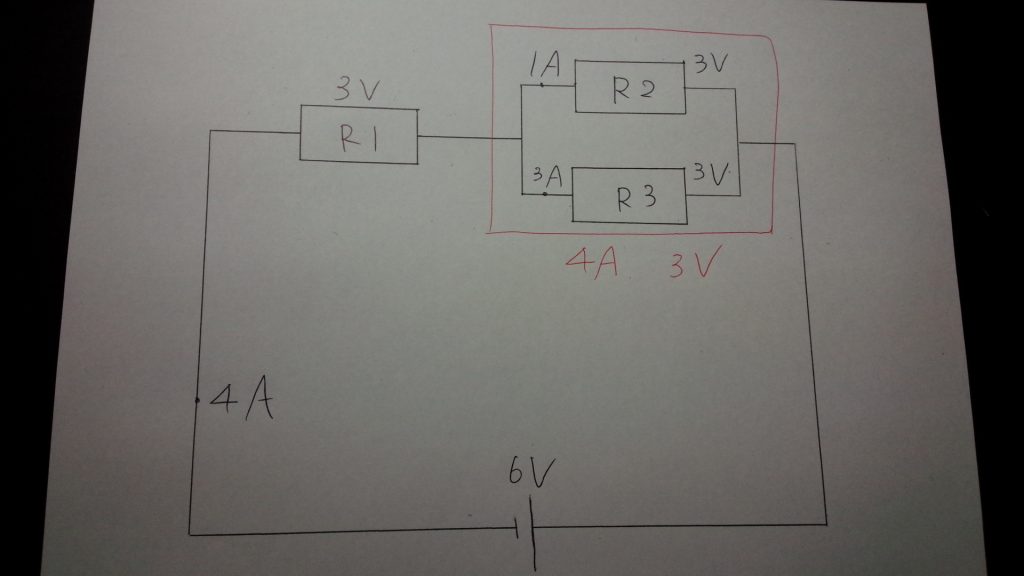
ここまで来れば、あとは簡単です。オームの法則から

$$３(Ｖ)\div３(Ａ) ＝ １ (Ω)$$

と求めることができます。

まとめ｜電気回路を解くときの“3つの鉄則”

電気回路の計算問題は、一見複雑に見えても

• 図に値を書き込む
• オームの法則と回路の性質を使う
• 複雑な部分はまとめて考える

この3つを意識するだけで、グッと解きやすくなります。

特に、図を描いて「見える化」することと、値を順に求めていくプロセスを丁寧に踏むことが、正確に解けるポイントです。

焦らず一つずつ整理しながら取り組めば、難問も必ずクリアできます。

今後もこのような「つまずきやすい単元をわかりやすく解説する記事」をアップしていきますので、ぜひチェックしてみてくださいね！

最後までお読みいただき、ありがとうございました。